sensiz olmaz
Kayıtlı Üye
Vektörlerde İşlemler
Vektör çeşitlerini tanımladıktan sonra, vektörler arasındaki işlemleri öğrenelim.
Skaler büyüklükleri kendi aralarında; toplama, çıkarma, çarpma ve bölme olarak bildiğimiz dört işlemle inceleriz. Vektörler arasındaki işlemlerde ise, bu büyüklüklerin yön ve doğrultu özelliklerinden kaynaklanan farklara dikkat etmek gerekir.
 Toplama İşlemi
Toplama İşlemi
Vektörlerde toplama işlemi şu üç yolla yapılabilir; çokgen, paralelkenar ve dik bileşenlere ayırma metodu.
a. Çokgen (uç uca ekleme) yöntemi
Vektörün yönü, doğrultusu ve büyüklüğü değiştirilmeden istediğimiz yere taşıyabiliyorduk. Bu özellikten yararlanarak ikiden çok vektörün toplamını bulabiliriz.
Çokgen (uç uca ekleme) yönteminde vektörlerin hangi sırayla toplandığının önemi yoktur. (şekil III (b)) Bir vektörü başlangıç vektörü olarak seçer diğer vektörleri sırasıyla, seçtiğimiz bu vektörün ucuna, diğer vektörün başlangıcı gelecek şekilde ekleriz.
Bir vektörün bittiği yere diğer vektörün başlangıcı gelecek şekilde işlem sürdürülür. İlk vektörün başlangıcı ile son vektörün bitiş noktasını birleştiren vektör ise bileşke vektörü verir. Bu yolla yön ve doğrultu bulunur, büyüklüğü ise geometri formülleriyle hesaplanır.
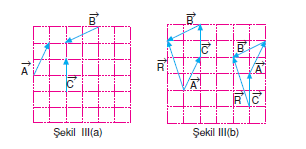 Not:Çokgen metodunda vektörlerin toplanma sırasının önemi yoktur.
Not:Çokgen metodunda vektörlerin toplanma sırasının önemi yoktur.
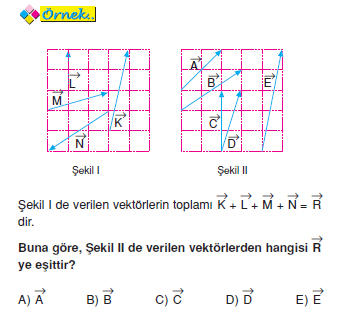
 Not:Vektörleri çokgen yöntemiyle topladığımızda başlangıç ve bitiş noktası aynı yer ise bu vektörel toplam sıfıra eşittir.
Not:Vektörleri çokgen yöntemiyle topladığımızda başlangıç ve bitiş noktası aynı yer ise bu vektörel toplam sıfıra eşittir.
(Bu özellik ileride göreceğimiz dengedeki sistemler için bize büyük kolaylıklar sağlayacaktır.(şekil 4 a,b,c)

Vektör çeşitlerini tanımladıktan sonra, vektörler arasındaki işlemleri öğrenelim.
Skaler büyüklükleri kendi aralarında; toplama, çıkarma, çarpma ve bölme olarak bildiğimiz dört işlemle inceleriz. Vektörler arasındaki işlemlerde ise, bu büyüklüklerin yön ve doğrultu özelliklerinden kaynaklanan farklara dikkat etmek gerekir.

Vektörlerde toplama işlemi şu üç yolla yapılabilir; çokgen, paralelkenar ve dik bileşenlere ayırma metodu.
a. Çokgen (uç uca ekleme) yöntemi
Vektörün yönü, doğrultusu ve büyüklüğü değiştirilmeden istediğimiz yere taşıyabiliyorduk. Bu özellikten yararlanarak ikiden çok vektörün toplamını bulabiliriz.
Çokgen (uç uca ekleme) yönteminde vektörlerin hangi sırayla toplandığının önemi yoktur. (şekil III (b)) Bir vektörü başlangıç vektörü olarak seçer diğer vektörleri sırasıyla, seçtiğimiz bu vektörün ucuna, diğer vektörün başlangıcı gelecek şekilde ekleriz.
Bir vektörün bittiği yere diğer vektörün başlangıcı gelecek şekilde işlem sürdürülür. İlk vektörün başlangıcı ile son vektörün bitiş noktasını birleştiren vektör ise bileşke vektörü verir. Bu yolla yön ve doğrultu bulunur, büyüklüğü ise geometri formülleriyle hesaplanır.



(Bu özellik ileride göreceğimiz dengedeki sistemler için bize büyük kolaylıklar sağlayacaktır.(şekil 4 a,b,c)




