sensiz olmaz
Kayıtlı Üye
Eşit İki Vektörün Toplamı İçin Özel Durumlar
Not:
İki vektörün arasındaki açı artarsa bileşkenin şiddeti azalır. Aralarındaki açı (q) ile bileşkenin büyüklü¤ü (R) ters orantılıdır. (180°
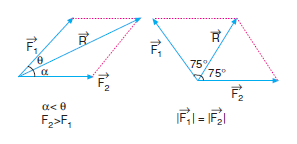
İki vektör ile bileşenleri arasında dikkat edilecek önemli noktalardan birisi şudur: Bileşke kuvvet, bileşenlerden şiddeti büyük olana daha yakındır. Bileşenler eşit şiddette ise bileşke açı ortay üzerindedir.
 İki vektörün bileşkesinin en büyük değeri vektörlerin skaler toplamına en küçük değeri ise skaler farklarına eşittir.
İki vektörün bileşkesinin en büyük değeri vektörlerin skaler toplamına en küçük değeri ise skaler farklarına eşittir.
Rmax = F1 + F2
Rmin = |F1 F2|
Buna göre, vektörlerinin bileşkesinin alacağı değerler
Rmin < R < Rmax
|F1 F2| < < F1 + F2
Üç vektörün bileşkesinin en büyük değeri vektörlerin skaler toplamına, minimum değeri ise
I. Küçük iki vektörün skaler toplamı büyük olan vektörden küçük ise büyük vektörden küçük iki vektörün farkına eşit
II. Küçük iki vektörün toplamı büyük vektöre eşit ya da büyük ise sıfırdır.
F1 > F2 > F3 ise
Rmax = F1 + F2 + F3
I. F2 + F3 < F1 ise Rmin = F1 (F2 + F3) II. F2 + F3 _> F1 ise
Rmin = 0 dır.







Not:
İki vektörün arasındaki açı artarsa bileşkenin şiddeti azalır. Aralarındaki açı (q) ile bileşkenin büyüklü¤ü (R) ters orantılıdır. (180°
İki vektör ile bileşenleri arasında dikkat edilecek önemli noktalardan birisi şudur: Bileşke kuvvet, bileşenlerden şiddeti büyük olana daha yakındır. Bileşenler eşit şiddette ise bileşke açı ortay üzerindedir.

Rmax = F1 + F2
Rmin = |F1 F2|
Buna göre, vektörlerinin bileşkesinin alacağı değerler
Rmin < R < Rmax
|F1 F2| < < F1 + F2
Üç vektörün bileşkesinin en büyük değeri vektörlerin skaler toplamına, minimum değeri ise
I. Küçük iki vektörün skaler toplamı büyük olan vektörden küçük ise büyük vektörden küçük iki vektörün farkına eşit
II. Küçük iki vektörün toplamı büyük vektöre eşit ya da büyük ise sıfırdır.
F1 > F2 > F3 ise
Rmax = F1 + F2 + F3
I. F2 + F3 < F1 ise Rmin = F1 (F2 + F3) II. F2 + F3 _> F1 ise
Rmin = 0 dır.










